Розв'язування задач «Паралельне проектування та його властивості»

 Перпендикулярність прямої і площини

Теорія:

Перпендикулярні прямі в просторі

Дві прямі називаються перпендикулярними, якщо кут між ними дорівнює 90°.

У просторі перпендикулярними називають не тільки прямі, що перетинаються, а й мимобіжні прямі, тому що ми кажемо про кут, який можуть утворити ці прямі, якщо їх розташувати в одній площині.

 

Так само як і в площині, в просторі перпендикулярні прямі $a$ і $b$ позначають $a\perp b$.

Якщо одна з двох паралельних прямих перпендикулярна до третьої прямої, то й інша перпендикулярна до цієї прямої.

Перпендикулярність прямої і площини

Пряма, що перетинає площину, називається перпендикулярною цій площині, якщо вона перпендикулярна кожній прямій, яка лежить у цій площині.

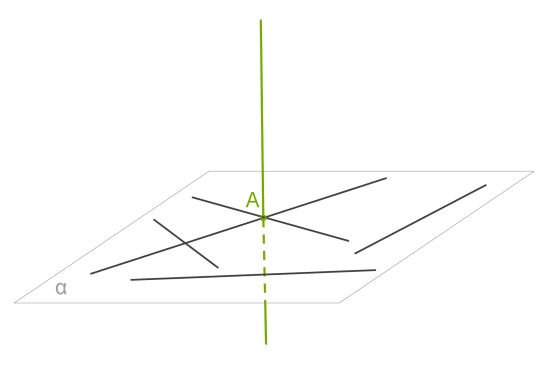
Перпендикулярність прямої і площини позначається як $a\perp \mathrm{\alpha }$.

Через будь-яку точку простору проходить пряма перпендикулярна даній площині, і до того ж тільки одна.

Ознака перпендикулярності прямої і площини.
Якщо пряма перпендикулярна двом прямим, що перетинаються у площині, то вона перпендикулярна цій площині.

 

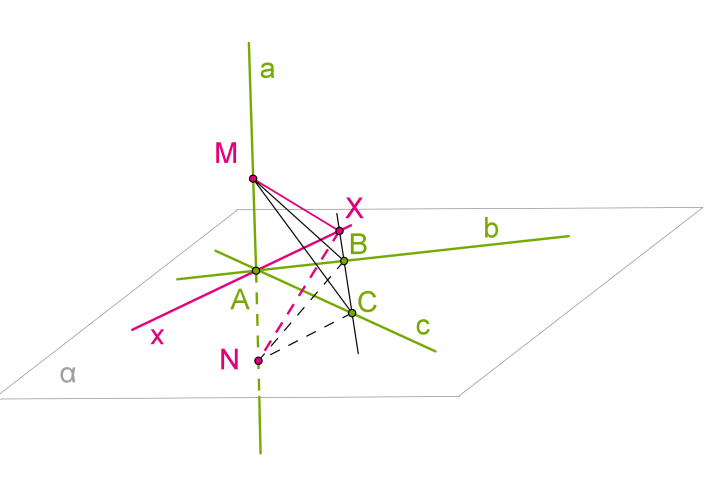
Доведення:

 

Нехай $a$ — пряма, перпендикулярна прямим $b$ і $c$ у площині. Проведемо пряму $a$ через точку $A$ перетину прямих $b$ і $c$. Доведемо, що пряма $a$ перпендикулярна площині, тобто кожній прямій в цій площині.

 

1. Проведемо довільну пряму $x$ через точку $A$ в площині і покажемо, що вона перпендикулярна прямій $a$. Проведемо в площині довільну пряму, що не проходить через точку $A$ і перетинає прямі $b$, $c$ і $x$. Нехай точками перетину будуть $B$, $C$ і $X$.

 

2. Відкладемо на прямій $a$ від точки $A$ в різні сторони рівні відрізки $AM$ і $AN$.

 

3. Трикутник $MCN$ рівнобедрений, оскільки відрізок $AC$ є висотою за умовою теореми і медіаною з побудови ($AM = AN$). З тієї ж причини трикутник $MBN$ теж рівнобедрений.

 

4. Отже, трикутники $MBC$ і $NBC$ рівні за трьома сторонами.

 

5. З рівності трикутників $MBC$ і $NBC$ випливає рівність кутів $MBX$ і $NBX$ і, отже, рівність трикутників $MBX$ і $NBX$ за двома сторонами та кутом між ними.

 

6. З рівності сторін $MX$ і $NX$ цих трикутників випливає, що трикутник $MXN$ рівнобедрений. Тому його медіана $XA$ є також висотою. А це і означає, що пряма $x$ перпендикулярна $a$. За визначенням пряма $a$ перпендикулярна площині.

 

Властивості перпендикулярних прямої та площини.

1. Якщо площина перпендикулярна одній з двох паралельних прямих, то вона перпендикулярна й інший.

2. Дві прямі, перпендикулярні одній і тій же площині, паралельні.

Закріплення матеріалу: Виконайте тести